Mechanics

Chapter 5: Force and Motion

Evan Luo

6 min read

1. What is a Force? Why does it matter?

  • A force is simply a push or a pull that one object (the agent) exerts on another.

  • Every force has magnitude (how strong) and direction → we treat forces as vectors.

  • Two broad families:

    1. Contact forces – need physical touch (e.g., friction, tension).
    2. Long-range forces – act at a distance (e.g., gravity, magnetism).

2. Net Force & Newton's Second Law

  • Net force = the vector sum of all forces acting on an object:

    F⃗net=∑iF⃗i\vec{F}_{\text{net}} = \sum_i \vec{F}_i

  • Experiments show:

    1. Acceleration a⃗\vec{a} grows in direct proportion to F⃗net\vec{F}_{\text{net}}.
    2. For a given F⃗net\vec{F}_{\text{net}}, heavier objects (more mass mm) accelerate less.

  • Combining both ideas gives Newton's 2nd Law:

    a⃗=F⃗netm\boxed{\vec{a} = \frac{\vec{F}_{\text{net}}}{m}}

    The acceleration points in the same direction as F⃗net\vec{F}_{\text{net}}.

  • Units:

    • Mass → kilograms (kg)
    • Force → newtons (N) – one newton is 1 kg⋅m/s21\ \text{kg} \cdot \text{m/s}^2.

3. Equilibrium & Newton's First Law

  • If no net force acts (∑F⃗=0\sum \vec{F} = 0), the object is in equilibrium:

    • At rest → it stays at rest.
    • Moving at constant velocity → it keeps that velocity.
    • Written as: a⃗=0\vec{a} = 0.

  • This is Newton's 1st Law ("law of inertia").

Key takeaway: motion itself needs no force to continue—only a change in motion needs force.

4. Everyday Forces to Recognise

SymbolForce nameDirection ruleUseful equationComment
F⃗G\vec{F}_GGravityStraight down (toward Earth's centre)FG=mgF_G = mgLong-range
F⃗sp\vec{F}_{\text{sp}}SpringToward spring's relaxed (equilibrium) length—Hooke's law appears later
T⃗\vec{T}TensionAlong (and pulling) the string/rope—Same at every point in an ideal rope
n⃗\vec{n}NormalPerpendicular to the surface—"Support" force
f⃗k\vec{f}_kKinetic frictionParallel & opposite to sliding motionfk=μknf_k = \mu_k nSurface must be sliding
f⃗s\vec{f}_sStatic frictionParallel & opposite to intended motionfs≤μsnf_s \leq \mu_s nHolds an object at rest

Free-body diagram: draw the object alone, then add each force with the correct direction and label. This makes the force equation easier to write correctly.

5. From Straight-Line Motion to Rotation – Introducing Torque

  • A force can also twist an object about a pivot.

  • We measure this twisting tendency with torque τ⃗\vec{\tau}:

    τ⃗=r⃗×F⃗\boxed{\vec{\tau} = \vec{r} \times \vec{F}}

    where:

    • r⃗\vec{r} = position vector from the pivot to where the force is applied,
    • ×\times = vector (cross) product.

  • Magnitude:

    τ=F rsin⁡ϕ=F d⊥\tau = F\,r\sin\phi = F\,d_\perp
    • ϕ\phi = angle between F⃗\vec{F} and r⃗\vec{r}.
    • d⊥d_\perp = shortest (perpendicular) distance from pivot to the force's line of action.

  • Sign convention (viewing +z coming out of the page):

    • Counter-clockwise (CCW) twist → +τ+\tau
    • Clockwise (CW) twist → −τ-\tau

  • Component trick: sometimes it is faster to resolve F⃗\vec{F} into xx- and yy-parts and add their torques:

    τ=Fx dy,⊥+Fy dx,⊥\tau = F_x\,d_{y,\perp} + F_y\,d_{x,\perp}

6. Net Torque

Just like forces, torques add:

τ⃗net=∑iτ⃗i\vec{\tau}_{\text{net}} = \sum_i \vec{\tau}_i

The net torque tells you the overall rotational effect of all forces on the object.

7. Quick Practice (try before peeking!)

A. The square plate shown on the left has a pivot point O at its centre. If F1=26 NF_1 = 26\ \text{N}, F2=14 NF_2 = 14\ \text{N}, and F3=18 NF_3 = 18\ \text{N}, what is the net torque?

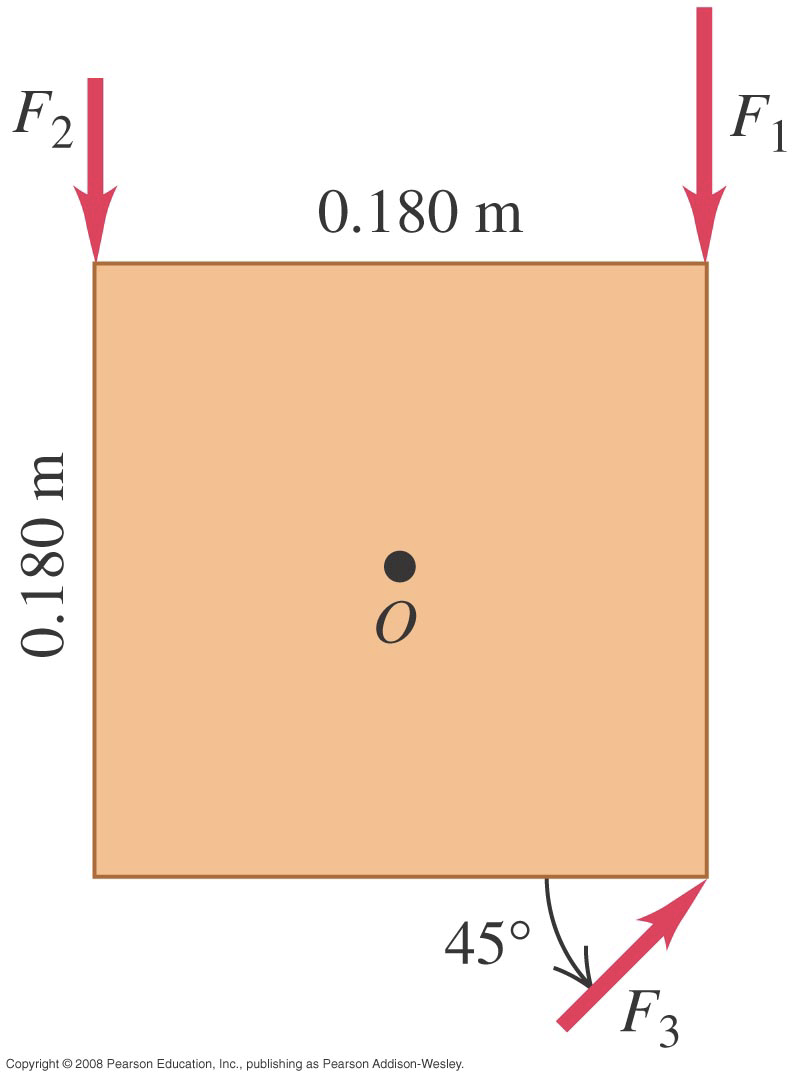
Square plate with forces

Using the torque formula τ=Frsin⁡ϕ\tau = Fr\sin\phi for each force:

For F1F_1 (26 N):

  • Distance from pivot to force application point: r=0.127 mr = 0.127\ \text{m}
  • Angle between force and position vector: ϕ=135∘\phi = 135^\circ
  • Torque: τ1=−(26 N)sin⁡135∘(0.127 m)=−2.33 Nm\tau_1 = -(26\ \text{N})\sin135^\circ(0.127\ \text{m}) = -2.33\ \text{Nm} (CW)

For F2F_2 (14 N):

  • Distance from pivot to force application point: r=0.127 mr = 0.127\ \text{m}
  • Angle between force and position vector: ϕ=135∘\phi = 135^\circ
  • Torque: τ2=(14 N)sin⁡135∘(0.127 m)=1.26 Nm\tau_2 = (14\ \text{N})\sin135^\circ(0.127\ \text{m}) = 1.26\ \text{Nm} (CCW)

For F3F_3 (18 N):

  • Distance from pivot to force application point: r=0.127 mr = 0.127\ \text{m}
  • Angle between force and position vector: ϕ=90∘\phi = 90^\circ
  • Torque: τ3=(18 N)sin⁡90∘(0.127 m)=2.29 Nm\tau_3 = (18\ \text{N})\sin90^\circ(0.127\ \text{m}) = 2.29\ \text{Nm} (CCW)

Net torque: τnet=τ1+τ2+τ3=−2.33 Nm+1.26 Nm+2.29 Nm=1.22 Nm\tau_{\text{net}} = \tau_1 + \tau_2 + \tau_3 = -2.33\ \text{Nm} + 1.26\ \text{Nm} + 2.29\ \text{Nm} = 1.22\ \text{Nm} (CCW)

Click to reveal

B. The pulley shown on the right has a mass of 5.0 kg5.0\ \text{kg} and a diameter of 30 cm30\ \text{cm}. The pulley has a pivot point O located half way between its center and its rim. A rope holding two 15 kg15\ \text{kg} masses wraps around the pulley. What is the net torque?

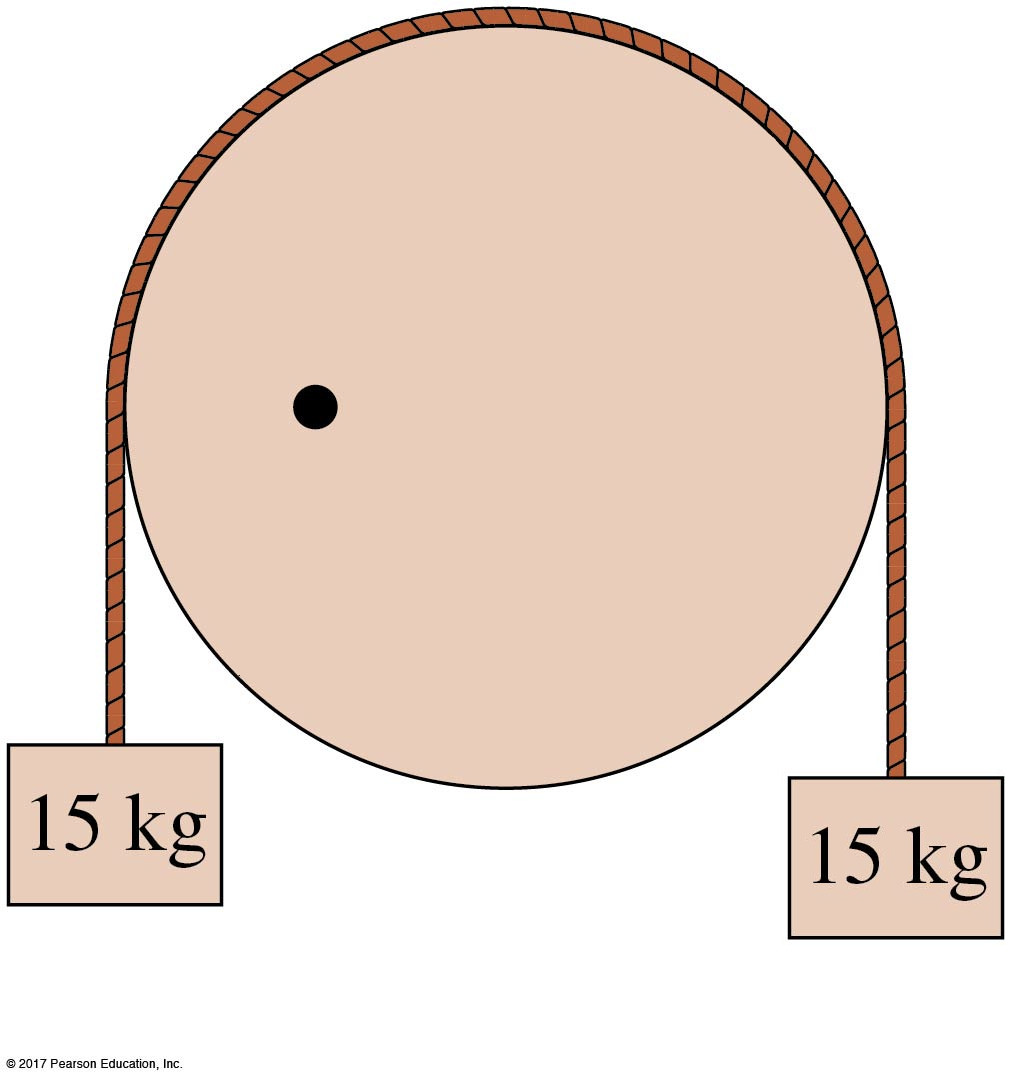
Pulley with masses

We need to calculate the torque from the pulley's weight and the two hanging masses:

For the 15 kg15\ \text{kg} mass on the left:

  • Force: F=mg=15 kg×9.8 m/s2=147 NF = mg = 15\ \text{kg} \times 9.8\ \text{m/s}^2 = 147\ \text{N}
  • Distance from pivot to force line of action: r=0.075 mr = 0.075\ \text{m}
  • Angle between force and moment arm: ϕ=90∘\phi = 90^\circ
  • Torque: τ1=(147 N)(0.075 m)sin⁡90∘=11.025 Nm\tau_1 = (147\ \text{N})(0.075\ \text{m})\sin90^\circ = 11.025\ \text{Nm} (CCW)

For the pulley's weight (5.0 kg5.0\ \text{kg}):

  • Force: F=mg=5.0 kg×9.8 m/s2=49 NF = mg = 5.0\ \text{kg} \times 9.8\ \text{m/s}^2 = 49\ \text{N}
  • Distance from pivot to center of mass: r=0.075 mr = 0.075\ \text{m}
  • Angle between force and moment arm: ϕ=90∘\phi = 90^\circ
  • Torque: τ2=−(49 N)(0.075 m)sin⁡90∘=−3.675 Nm\tau_2 = -(49\ \text{N})(0.075\ \text{m})\sin90^\circ = -3.675\ \text{Nm} (CW)

For the 15 kg15\ \text{kg} mass on the right:

  • Force: F=mg=15 kg×9.8 m/s2=147 NF = mg = 15\ \text{kg} \times 9.8\ \text{m/s}^2 = 147\ \text{N}
  • Distance from pivot to force line of action: r=0.225 mr = 0.225\ \text{m}
  • Angle between force and moment arm: ϕ=90∘\phi = 90^\circ
  • Torque: τ3=−(147 N)(0.225 m)sin⁡90∘=−33.075 Nm\tau_3 = -(147\ \text{N})(0.225\ \text{m})\sin90^\circ = -33.075\ \text{Nm} (CW)

Net torque: τnet=τ1+τ2+τ3=11.025 Nm+(−3.675 Nm)+(−33.075 Nm)=−25.725 Nm\tau_{\text{net}} = \tau_1 + \tau_2 + \tau_3 = 11.025\ \text{Nm} + (-3.675\ \text{Nm}) + (-33.075\ \text{Nm}) = -25.725\ \text{Nm} (CW)

Click to reveal

8. Key Points to Remember

  1. Draw a free-body diagram first—it clarifies both linear and rotational problems.
  2. For straight-line motion, relate F⃗net\vec{F}_{\text{net}} to a⃗\vec{a} via Newton's 2nd law.
  3. For rotation, replace forces with torques about the chosen pivot, then sum them.
  4. Zero net force   ⟹  \implies no linear acceleration; zero net torque   ⟹  \implies no angular acceleration.
  5. Sign conventions (for torque directions) keep results consistent—pick one and stick to it.

Feel free to ask for more examples, deeper derivations, or practice problems!

Back to Mechanics

0 reads

Last edited