Chapter 6: Linear Dynamics

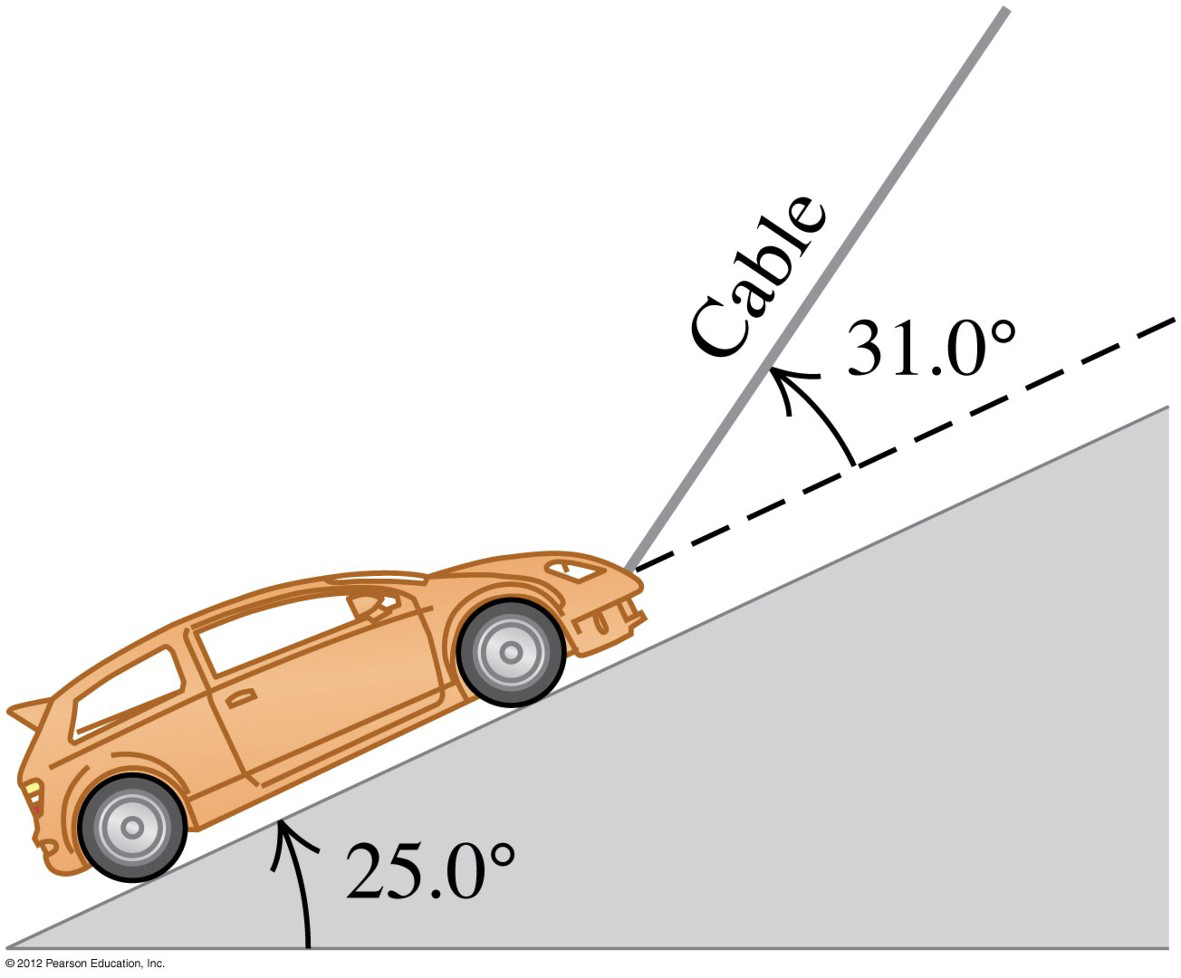
Solution:

First, we need to identify all forces and establish a coordinate system:

• Weight (gravity): $F_G = (1130 \text{ kg})(9.8 \text{ m/s}^2) = 11074 \text{ N}$ acting straight down
• Tension ($T$): Acting at 31° above the ramp surface
• Normal force ($n$): Perpendicular to the ramp surface

Let's choose our coordinate system with the x-axis parallel to the ramp (downhill) and the y-axis perpendicular to the ramp.

For equilibrium: $\sum F_x = 0$ and $\sum F_y = 0$

Step 1: Find the components of gravity. Since the ramp is at 25° above horizontal, the angle between the weight and the negative y-axis is 65°.

• $F_{Gx} = -F_G \cos 65° = -(11074 \text{ N})(\cos 65°) = -4680 \text{ N}$
• $F_{Gy} = -F_G \sin 65° = -(11074 \text{ N})(\sin 65°) = -10036 \text{ N}$

Step 2: Write the equilibrium equations. $\sum F_x = 0$: $-4680 \text{ N} + T\cos 31° = 0$ $\sum F_y = 0$: $-10036 \text{ N} + T\sin 31° + n = 0$

Step 3: Solve for the tension (part a). $T\cos 31° = 4680 \text{ N}$ $T = \frac{4680 \text{ N}}{\cos 31°} = 5460 \text{ N}$

Step 4: Solve for the normal force (part b). $n = 10036 \text{ N} - (5460 \text{ N})(\sin 31°)$ $n = 10036 \text{ N} - 2812 \text{ N}$ $n = 7224 \text{ N}$

Therefore: (a) The tension in the cable is 5460 N. (b) The normal force exerted by the ramp is 7224 N.

Solution:

We can divide this problem into two phases: accelerating (engine on) and coasting (engine off).

Phase 1: Accelerating (engine on)

• Mass: $m = 8.0 \times 10^4$ kg
• Thrust force: $F = 1.20 \times 10^6$ N
• Initial velocity: $v₀ = 0$ m/s
• Time: $t = 20$ s

Apply Newton's Second Law to find acceleration: $\sum F_x = ma_x$ $F_{thrust} = ma_x$ $1200000 \text{ N} = (80000 \text{ kg})a_x$ $a_x = 15 \text{ m/s}^2$

Final velocity after 20 seconds: $v_f = v_i + a_x \Delta t$ $v_f = 0 + (15 \text{ m/s}^2)(20 \text{ s})$ $v_f = 300 \text{ m/s}$

Distance traveled during acceleration: $x = v_i t + \frac{1}{2}a_x t^2$ $x = 0 + \frac{1}{2}(15 \text{ m/s}^2)(20 \text{ s})^2$ $x = \frac{1}{2}(15)(400) = 3000 \text{ m} = 3 \text{ km}$

Phase 2: Coasting (engine off)

• Velocity: v = 300 m/s (constant)
• Remaining distance: 12 km - 3 km = 9 km = 9000 m

Time for coasting phase: $\Delta t = \frac{d}{v} = \frac{9000 \text{ m}}{300 \text{ m/s}} = 30 \text{ s}$

Total trip time: $t_{total} = 20 \text{ s} + 30 \text{ s} = 40 \text{ s}$

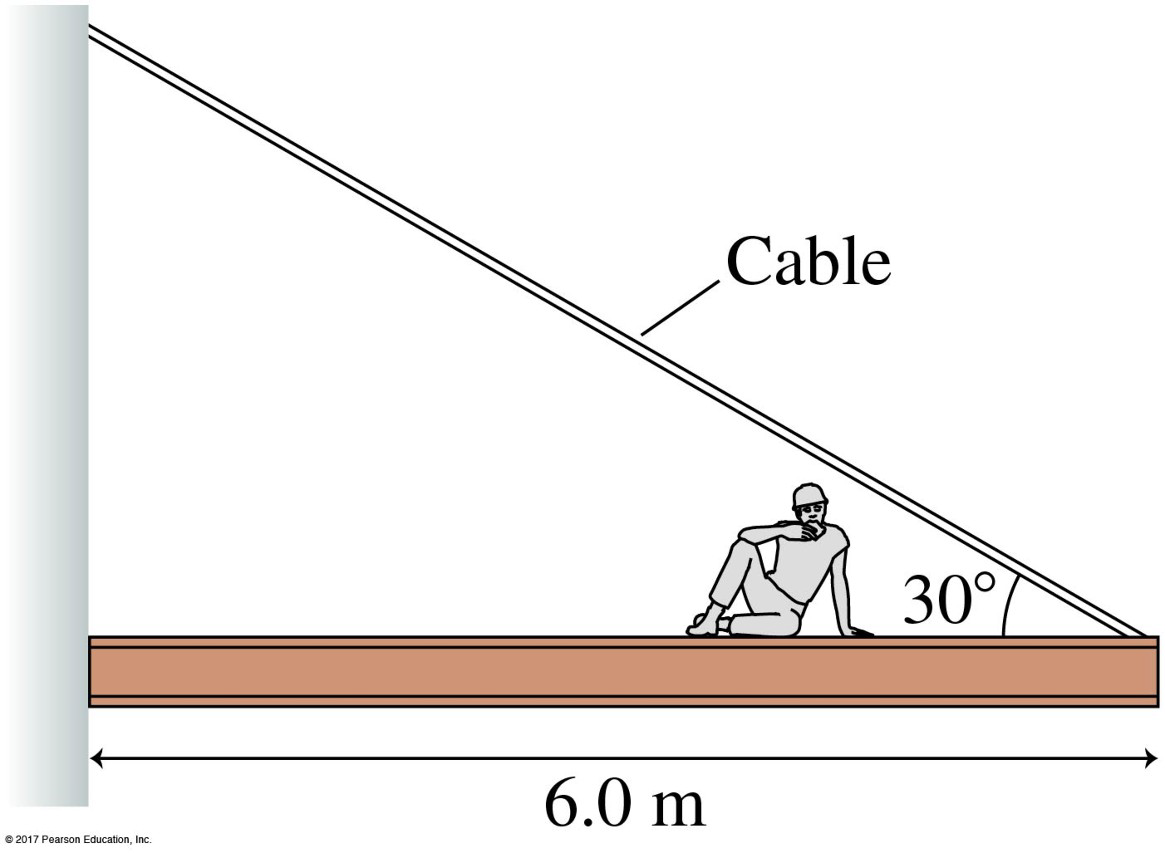
Solution:

This is a rotational equilibrium problem. We'll calculate the torques about the wall attachment point (pivot).

Step 1: Identify the forces and their moment arms.

• Beam weight: $F_{GB} = (1450 \text{ kg})(9.8 \text{ m/s}^2) = 14210 \text{ N}$, acting at the center of the beam (3.0 m from the wall)
• Worker's weight: $F_{GW} = (80 \text{ kg})(9.8 \text{ m/s}^2) = 784 \text{ N}$, acting 4.0 m from the wall
• Cable tension: $T$, acting 6.0 m from the wall at 30° angle

Step 2: Calculate the torques. Taking counterclockwise as positive:

• Beam torque: $\tau_B = -(14210 \text{ N})(3.0 \text{ m})(\sin 90°) = -42630 \text{ Nm}$ (CW)
• Worker torque: $\tau_W = -(784 \text{ N})(4.0 \text{ m})(\sin 90°) = -3136 \text{ Nm}$ (CW)
• Cable torque: $\tau_C = T(6.0 \text{ m})(\sin 30°) = T(3.0 \text{ m})$ (CCW)

Step 3: Apply the rotational equilibrium condition. $\sum \tau = 0$ $\tau_B + \tau_W + \tau_C = 0$ $-42630 \text{ Nm} - 3136 \text{ Nm} + T(3.0 \text{ m}) = 0$

Step 4: Solve for the tension. $T(3.0 \text{ m}) = 42630 \text{ Nm} + 3136 \text{ Nm}$ $T(3.0 \text{ m}) = 45766 \text{ Nm}$ $T = \frac{45766 \text{ Nm}}{3.0 \text{ m}} = 15255 \text{ N}$

Therefore, the tension in the cable is 15255 N.

Solution:

We can solve this by analyzing the forces before and after the box falls off.

Initial situation (truck with box):

• Total mass: $m_{total} = 7500$ kg
• Moving at constant speed up the slope: $a = 0$ $m/s^2$
• Slope angle: $15^\circ$

For motion at constant speed up the slope, the engine force must exactly balance the component of gravity pulling down the slope.

The weight of the truck and box: $F_G = (7500 \text{ kg})(9.8 \text{ m/s}^2) = 73500 \text{ N}$ acting straight down.

Component of weight parallel to the slope (pulling down):

• $F_{Gx} = F_G \sin 15° = (73500 \text{ N})(\sin 15°) = 19023 \text{ N}$

For constant speed up the slope, the engine force must equal this:

• $F_{engine} = 19023 \text{ N}$

After the box falls off:

• Truck mass: $m_T$ (what we're solving for)
• Box mass: $m_B = 7500 \text{ kg} - m_T$
• Truck acceleration: $a = 2.0 \text{ m/s}^2$ up the slope
• Engine force remains the same: $F_{engine} = 19023 \text{ N}$

Now we apply Newton's Second Law to the truck after the box falls off: $\sum F = m_T a$

The forces acting parallel to the slope:

• Engine force: $+19023 \text{ N}$ (up the slope)
• Component of truck weight: $-m_T g \sin 15° = -m_T(9.8 \text{ m/s}^2)(\sin 15°) = -m_T(2.536 \text{ m/s}^2)$ (down the slope)

Rearranging to solve for $m_T$: $19023 \text{ N} = m_T(2.0 \text{ m/s}^2) + m_T(2.536 \text{ m/s}^2)$ $19023 \text{ N} = m_T(4.536 \text{ m/s}^2)$ $m_T = \frac{19023 \text{ N}}{4.536 \text{ m/s}^2} = 4193 \text{ kg}$

Therefore, the mass of the box is: $m_B = 7500 \text{ kg} - 4193 \text{ kg} = 3307 \text{ kg}$